Joint Error Rate calibration
Simulations for one and two-sample tests
P. Neuvial
2018-03-27
Source:vignettes/jointErrorRateCalibration_simulations.Rmd
jointErrorRateCalibration_simulations.RmdThis vignettes illustrates the following points
- simulation of one- and two-sample Gaussian equi-correlated observations
- computation of test statistics by randomization
- calibration of Joint-Family-Wise Error Rate (JER) thresholds
We start with two-sample tests because we believe they are used more frequently.
library("sanssouci")
#set.seed(0xBEEF) # for reproducibility
library("ggplot2")Parameters:
m <- 5e2
n <- 30
pi0 <- 0.8
rho <- 0.3
SNR <- 3We use the function SansSouciSim to generate Gaussian
equi-correlated samples. We then ‘fit’ the resulting SansSouci
object
Two-sample tests
Simulation
obj <- SansSouciSim(m, rho, n, pi0, SNR = SNR, prob = 0.5)
obj## 'SansSouci' object:
## Number of hypotheses: 500
## Number of observations: 30
## 2-sample data
##
## Truth:
## 100 false null hypotheses (signals) out of 500 (pi0=0.8)We perform JER calibration using the linear (Simes) template \(\mathfrak{R(\lambda)}=(R_1(\lambda),\) \(\ldots,R_K(\lambda)\), where for \(1 \leq k \leq K\)
\[R_k(\lambda) = \left\{i\in \{1, \dots , m\}\::\: \bar{\Phi}(Z_i) > \frac{\lambda k}{m} \right\}\,\]
where \(\bar{\Phi}\) is the cdf of the \(\mathcal{N}(0,1)\) distribution. Note that \(p_i = \bar{\Phi}(Z_i)\) is the one-sided \(p\)-value associated to the test statistics \(Z_i\).
Calibration
B <- 1000
alpha <- 0.2
cal <- fit(obj, alpha = alpha, B = B, family = "Simes")
cal## 'SansSouci' object:
## Number of hypotheses: 500
## Number of observations: 30
## 2-sample data
##
## Truth:
## 100 false null hypotheses (signals) out of 500 (pi0=0.8)
## Parameters:
## Test function: rowWelchTests
## Number of permutations: B=1000
## Significance level: alpha=0.2
## Reference family: Simes
## (of size: K=500)
##
## Output:
## Calibration parameter: lambda=0.2051593The output of the calibration is the following SansSouci
object. In particular:
-
cal$inputcontains the input simulated data (and the associated truth) -
cal$paramcontains the calibration parameters -
cal$outputcontains the output of the calibration, including-
p.values: \(m\) test statistics calculated by permutation -
thr: A JER-controlling family of \(K\) (here \(K=m\)) elements -
lambda: the \(\lambda\)-calibration parameter
-
Because we are under positive equi-correlation, we expect \(\lambda > \alpha\) for the Simes family.
cal$output$lambda## 20%
## 0.2051593
cal$output$lambda > alpha## 20%
## TRUEPost hoc confidence bounds
The fitted SansSouci object contains post hoc confidence
bounds:
## x label stat bound
## 1 1 Simes TP 1
## 2 2 Simes TP 2
## 3 3 Simes TP 3
## 4 4 Simes TP 4
## 5 5 Simes TP 5
## 6 6 Simes TP 6We compare it to the true number of false positives among the most significant items, and to the Simes bound without calibration
cal0 <- fit(obj, alpha = alpha, B = 0, family = "Simes")
oracle <- fit(obj, alpha = alpha, family = "Oracle")
confs <- list(Simes = predict(cal0, all = TRUE),
"Simes+calibration" = predict(cal, all = TRUE),
"Oracle" = predict(oracle, all = TRUE))
plotConfCurve(confs, xmax = 200)
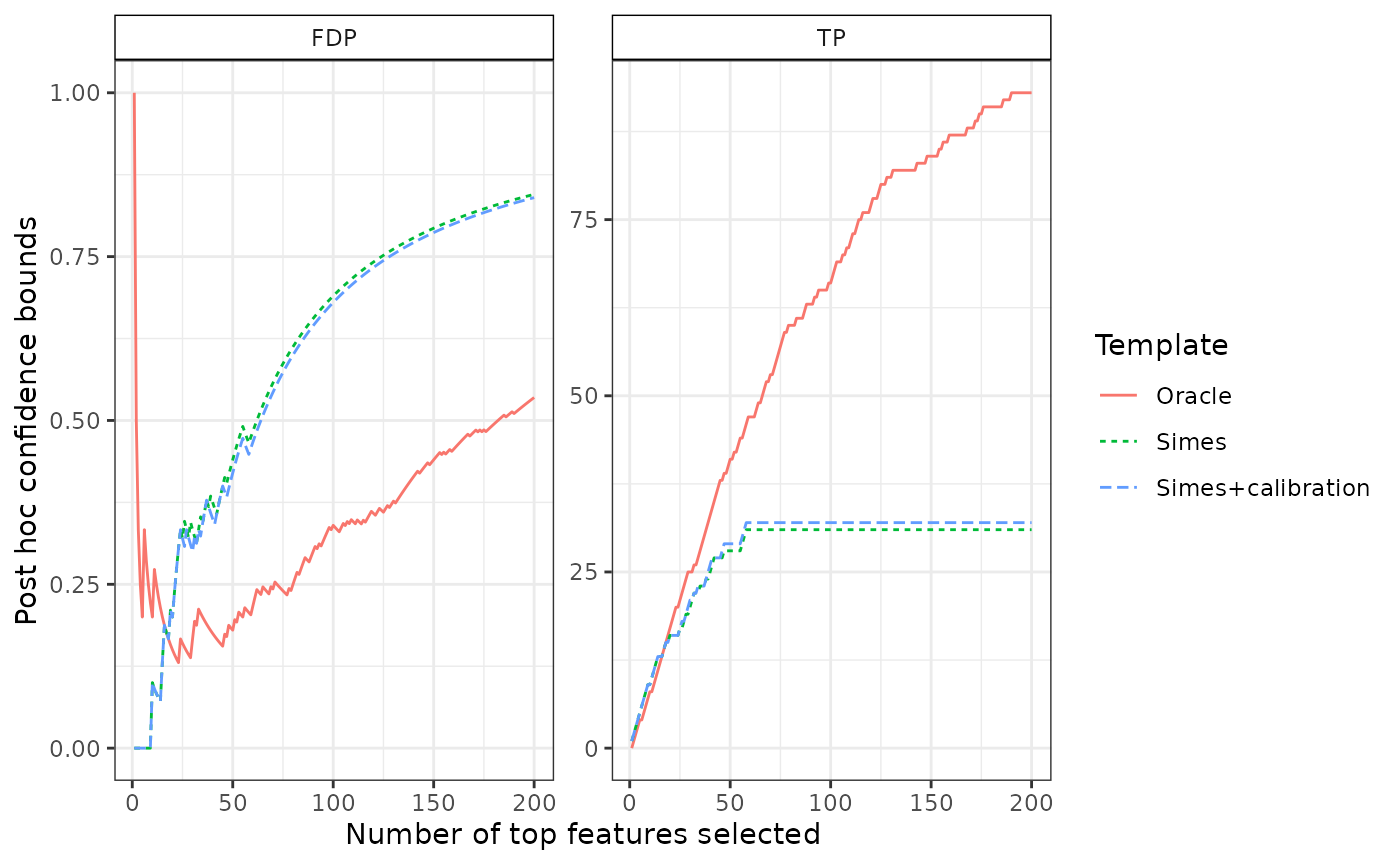
One sample tests
The code is identical, except for the line to generate the
observations (where we do not specify a probability of belonging to one
of the two populations using the prob argument); moreover
it is not necessary to specify a vector of categories ‘categ’ in
‘calibrateJER’.
obj <- SansSouciSim(m, rho, n, pi0, SNR = SNR)
obj## 'SansSouci' object:
## Number of hypotheses: 500
## Number of observations: 30
## 1-sample data
##
## Truth:
## 100 false null hypotheses (signals) out of 500 (pi0=0.8)
cal <- fit(obj, alpha = alpha, B = B, family = "Simes")
cal## 'SansSouci' object:
## Number of hypotheses: 500
## Number of observations: 30
## 1-sample data
##
## Truth:
## 100 false null hypotheses (signals) out of 500 (pi0=0.8)
## Parameters:
## Test function: rowZTests
## Number of permutations: B=1000
## Significance level: alpha=0.2
## Reference family: Simes
## (of size: K=500)
##
## Output:
## Calibration parameter: lambda=0.382704Again we expect \(\lambda > \alpha\).
Confidence curves
The associated confidence curves are displayed below:
cal0 <- fit(obj, alpha = alpha, B = 0, family = "Simes")
oracle <- fit(obj, alpha = alpha, family = "Oracle")
confs <- list(Simes = predict(cal0, all = TRUE),
"Simes+calibration" = predict(cal, all = TRUE),
"Oracle" = predict(oracle, all = TRUE))
plotConfCurve(confs)
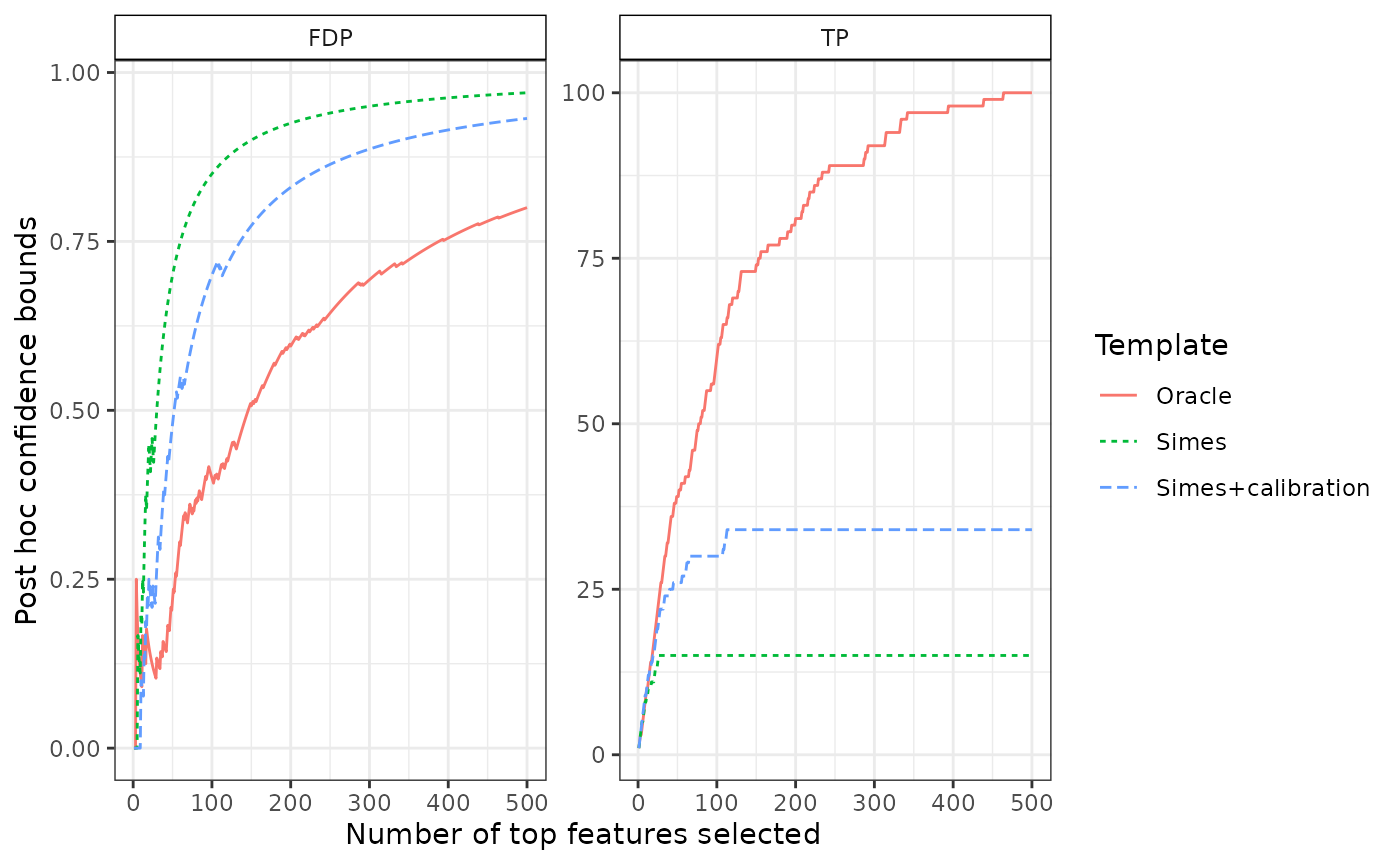
Session information
## R version 4.4.1 (2024-06-14)
## Platform: x86_64-pc-linux-gnu
## Running under: Ubuntu 22.04.4 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
## LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.20.so; LAPACK version 3.10.0
##
## locale:
## [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
## [4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
## [7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
## [10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
##
## time zone: UTC
## tzcode source: system (glibc)
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] ggplot2_3.5.1 sanssouci_0.13.0
##
## loaded via a namespace (and not attached):
## [1] Matrix_1.7-0 gtable_0.3.5 jsonlite_1.8.8 highr_0.11
## [5] compiler_4.4.1 Rcpp_1.0.12 jquerylib_0.1.4 systemfonts_1.1.0
## [9] scales_1.3.0 textshaping_0.4.0 yaml_2.3.8 fastmap_1.2.0
## [13] lattice_0.22-6 R6_2.5.1 labeling_0.4.3 generics_0.1.3
## [17] knitr_1.47 tibble_3.2.1 desc_1.4.3 munsell_0.5.1
## [21] bslib_0.7.0 pillar_1.9.0 rlang_1.1.4 utf8_1.2.4
## [25] cachem_1.1.0 xfun_0.45 fs_1.6.4 sass_0.4.9
## [29] memoise_2.0.1 cli_3.6.3 withr_3.0.0 pkgdown_2.0.9
## [33] magrittr_2.0.3 matrixTests_0.2.3 digest_0.6.35 grid_4.4.1
## [37] lifecycle_1.0.4 vctrs_0.6.5 evaluate_0.24.0 glue_1.7.0
## [41] farver_2.1.2 ragg_1.3.2 fansi_1.0.6 colorspace_2.1-0
## [45] rmarkdown_2.27 purrr_1.0.2 pkgconfig_2.0.3 matrixStats_1.3.0
## [49] tools_4.4.1 htmltools_0.5.8.1